


Bewegt sich ein Körper, der im Ruhezustand die Masse m0 hat, mit einer extrem hohen Geschwindigkeit v, die mit der Geschwindigkeit des Lichts c vergleichbar ist, dann wirkt anstelle der Ruhemasse m0 die relativistische Masse m (v):
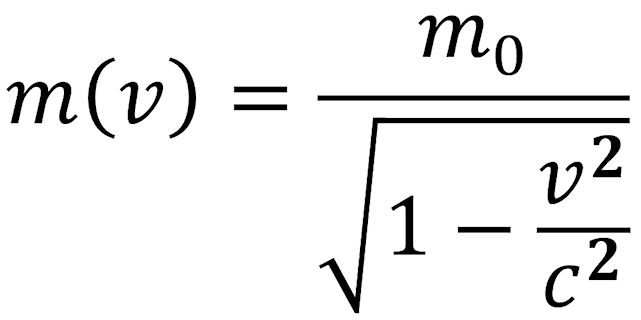
Ist v / c << 1, kann man die Wurzel im Nenner obiger Gleichung in
eine Reihe entwickeln und nach dem zweiten Glied abbrechen.
Es ergibt sich als Näherung
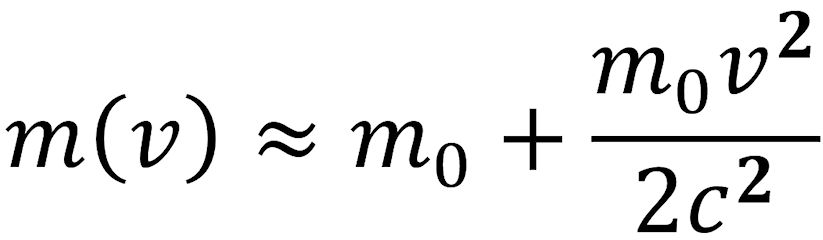
Der Quotient m0v2/2 im rechten Summanden entspricht der durch die hohe Geschwindigkeit gewonnenen kinetischen Energie ΔE. Die zur Ruhemasse zusätzliche Masse Δm ist also gleich ΔE/c2. Solche Überlegungen führten Albert Einstein (Bild oben) zu einem Postulat, das einen Grundpfeiler seiner speziellen Relativitätstheorie darstellt:
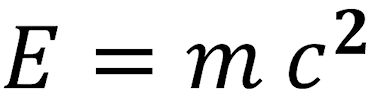
Bereits 1905 war damit die grundlegende Formel für die ein halbes Jahrhundert später aufkommende Elektrizitätserzeugung durch Kernenergie gefunden worden.
Bei Kernfusion und Kernspaltung ergibt sich ein Massendefekt Δm zwischen Ausgangsprodukt und Endprodukt. Das erzeugt nach der obigen Einstein'schen Beziehung einen Energiegewinn E = Δmc2 mit c als Lichtgeschwindigkeit. Aus einem Massendefekt von 1 kg erhält man die Energie von etwa 9 ×1016J, was äquivalent zur Verbrennung von reichlich 3 Millionen Tonnen Kohle wäre. Die Gewinnung elektrischer Energie durch Kernspaltung ist weit verbreitet, während sich die Energiegewinnung durch Kernfusion noch im Entwicklungsstadium befindet, siehe Kerkraftwerke.
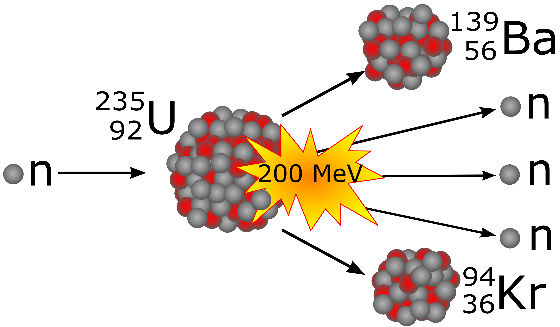
Die Uranspaltung geht vom nicht-stabilen Isotop U-235 aus, das durch Beschuss mit langsamen Neutronen in U-236 überführt wird. Das zerfällt sofort unter Bildung von Ba-139 und Kr-94 und Neutronen, wobei der Massendefekt in die Energie von etwa 200 MeV umgesetzt wird. In technischen Prozessen entstehen neben der Energie im Mittel 2,5 Neutronen. Das rechte Schema entspricht der klassischen Erklärung von Lise Meitner und basiert auf einer Abbildung von Wikimedia.
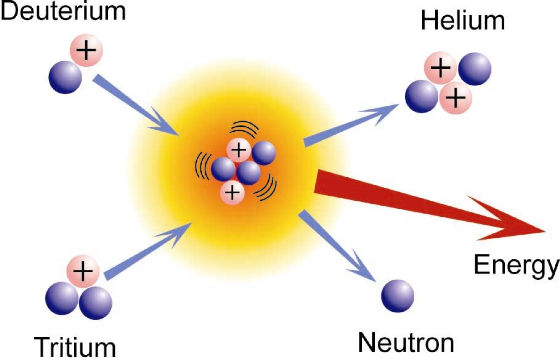
Bei der Fusion eines Deuterium- und eines Tritiumkerns entstehen ein 4He2+ (α-Teilchen) und ein Neutron. Vor allem wird aber dabei 17,6 MeV Energie ausgestrahlt. Die rechte aus den Internetseiten der EU-Organisation Fusion for Energy entnommene Abbildung zeigt die Fusionsreaktion
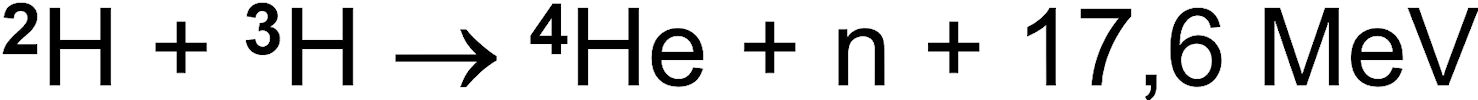
Hauptproblem bei der Fusion auf der Erde ist die extreme Reaktionstemperatur. Bei mehr als zehn Millionen Grad muss das Plasma auf einer stabilen Position fern von jeglichem Material bleiben.
Im Inneren der Sonne herrschen solche Temperaturen. Der Hauptprozess auf der Sonne ist die Proton-Proton-Reaktion. Zuerst fusionieren zwei Wasserstoffkerne 1H+ (Protonen) zu einem Deuteriumkern 2H+, wobei durch die Umwandlung eines Protons in ein Neutron ein Positron e+ und ein Elektronneutrino νe frei wird:

Das entstandene Deuterium reagiert mit einem weiteren Proton, und es entsteht das leichte Helium-Isotop 3He2+ und ein Gammaquant:
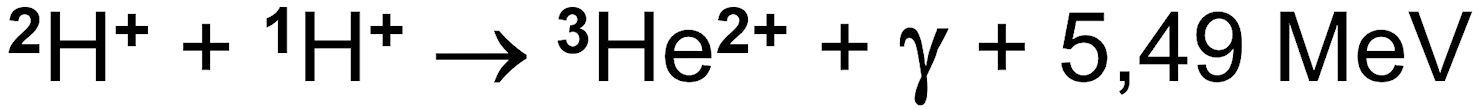
Schließlich fusionieren zwei Heliumkerne 3He2+ zu 4He2+ (α-Teilchen). Dabei werden zwei Protonen frei, die für weitere Reaktionsschritte zur Verfügung stehen:
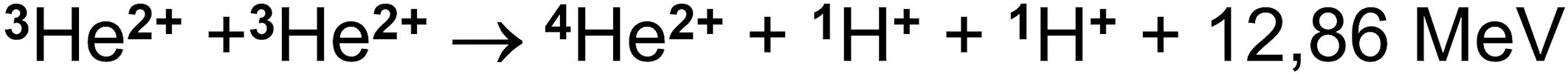
Die Kernfusion in der Sonne ist Grundlage der meisten Energiequellen auf der Erde. Die auf den rechten Seiten obiger Gleichungen aufgeführten Energien werden ausgestrahlt, was auch in der nächsten Milliarde von Jahren so bleiben wird. Die technische Energieerzeugung auf der Erde ist auf der Seite Kernkraftwerke dargestellt.