Wärmenergie

In der Wärmelehre entspricht die Wärmemenge Q einer Energieform, die als thermische oder Wärmeenergie der ungeordneten Bewegung mikroskopischer Teilchen zuzuordnen ist und mit zunehmender Temperatur T steigt. Robert von Mayer fand im Jahre 1842 den 1. Hauptsatz der Thermodynamik, der heute so formuliert wird:

Führt man einem System die Wärmemenge dQ zu und verrichtet die äußere Arbeit dW,
so nimmt die Zustandsgröße innere Energie U
um dU zu, und es gilt

Die Umsetzung thermischer Energie in Arbeit wird durch den 2. Hauptsatz der Thermodynamik eingeschränkt, den Carnot bereits im Jahre 1824 gefunden hatte. Die heute gebräuchliche Formulierung ist:

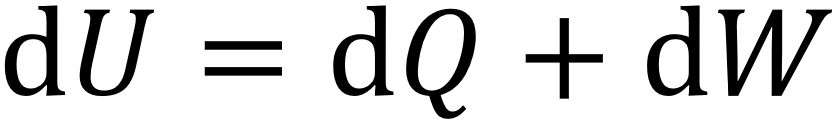
In einem abgeschlossenen thermodynamischen System kann die Entropie S nur zunehmen
oder bei umkehrbaren (reversiblen) Prozessen höchstens gleich bleiben:

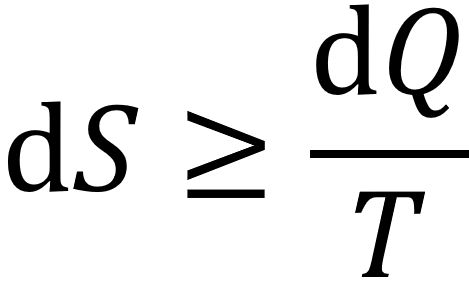
Eine allgemein verständliche Aussage mit gleichem Inhalt ist, dass es ist nicht möglich ist, eine Maschine zu bauen, die kontinuierlich Arbeit leistet, indem sie einem System Wärme entzieht. Die Formulierung von Kelvin und Planck lautet:
"Es gibt keine Zustandsänderung, deren einzige Ergebnisse das Abkühlen eines Körpers und das Heben eines Gewichtes sind." Dem ersten Hauptsatz der Thermodynamik würde diese Maschine nicht widersprechen. Man nennt eine solche Kraftmaschine, die nur Wärme verbraucht und vollständig in mechanische oder elektrische Energie umwandelt, ein Perpetuum mobile zweiter Art. Deshalb kann man den zweiten Hauptsatz auch so formulieren: "Ein Perpetuum mobile zweiter Art ist unmöglich."

Der reversible Carnot'sche Kreisprozess beschreibt
eine kontinuierlich arbeitende Maschine mit dem nach dem 2. Hauptsatz maximalen Wirkungsgrad. Im Druck-Volumen-Diagramm (p-V) eines idealen Gases im Bild links wird von zwei Isothermen (Linien gleicher Temperatur) und zwei Isentropen (Linien gleicher Entropie) die Fläche der Nutzenergie (Exergie) eingeschlossen. Die zugeführte Wärme ist durch Heizung aufzubringen, die abgeführte Wärme geht durch Kühlung verloren. Weil die Isentropen reversibel durchlaufene Adiabaten sind, das heißt,
es findet kein Energieaustausch mit der Umgebung statt, haben wir im Kreis 1, 2, 3, nach 4 zuerst isotherme Kompression und Wärmeabgabe ans Kühlmittel (Kondensattemperatur T_c), danach adiabatische Kompression, danach isotherme Expansion und Wärmeaufnahme aus dem geheizten Reservoir (Temperatur T_h) und zuletzt adiabatische Expansion. 

Beim Durchlaufen der Isotherme wird die Wärme q_zu = T_h DS zugeführt, beim Kühlen die Wärme q_ab = T_c DS abgeführt. Die Differenz  entspricht der geleisteten Arbeit W_Nutz.  Damit ist der Wirkungsgrad h, das Verhältnis von Nutzenergie zur aufgewendeten Energie,

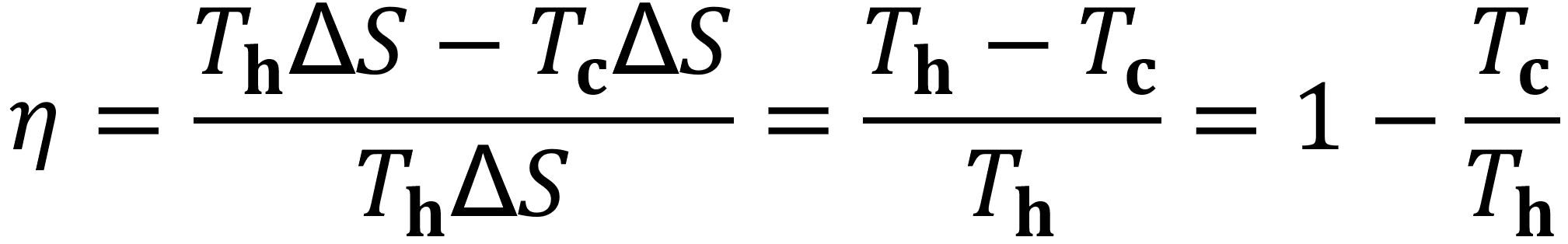
Nimmt man als Kühlmitteltemperatur 20 °C und als heiße Temperatur siedendes Wasser bei 100 °C, ergibt sich aus
293,15 K / 373,15 K » 0,79 ein Wirkungsgrad von 21 %. Reale Kreisprozesse haben einen niedrigeren Wirkungsgrad
als der Carnot-Prozess.